理論

実験の話にひきつづいて、理論というものの意味について、考えてみることにしよう。

実験と理論とは、車の両輪のようなものであるとよくいわれるが、自然科学の正道は、実験と理論とが並行して進んでいくところにある。この両者のバランスによって、自然科学は発達する。このことは、もちろん前から誰でもいっていることであるが、ここでは理論というものの意味を、もう少し立ちいって考えてみよう。

実験によって、もののある具体的な性質、あるいは現象間のつらなりが知られたとしても、それだけでは学問とはいえない。いわゆる学問の定義の中にはいるには、そいういう知識に、ある体系が組立てられなければならない。体系ができてはじめてそれが役に立つことになる。

ところで、いろいろ雑多な個々の知識に体系をつけるという場合に、二つのやり方がある。その一つは、こういう知識を、整理することである。たとえば、分類するということも、一つの体系をつくることである。事実そういうことも、決してばかにはならないのであって、古典的な動物学や植物学の中で、いわゆる分類学といわれている部門なども、案外役に立っているのである。この頃は、そういう学問があまりはやらないので、何か初歩の学問のように思われている傾向もあるが、実際にはああいう知識が、大いに役に立っているのである。

しかしそればかりでは、もちろん今日われわれのいう学問の体系にはならない。今日学問の体系といわれているものは、いろいろな個々の知識を整理するだけでなく、綜合したものである。自然現象というものは、複雑ではあるが、連続した融合体である。それをいろいろな方面から見て、いろいろな知識を得る。そういうたくさんの知識を、一つの綜合した知識に組み立てることが体系をつくることである。ところでそういう体系をつくることによって、何か得るところがあるかというと、それは大いにあるのである。多くの知識をただ寄せ集めたばかりでは、あまり役に立たない。しかしほんとうにこれを有機的に綜合すると、学問の次の発展をうながすという、非常に大切な役目をすることになる。

発展といっても、いろいろな意味があるが、その中で一番はっきりしているのは、いわゆる予言ができることである。もっとも予言がぴったりできる場合はめったにないが、少なくとも方向を指示できるということは、始終ある。いろいろな知識を綜合することによって、抜けている部分に気がついたり、あるいは先に発展しそうな方面が分ったりする。そしてその方向に新しい研究を踏み出す。そういうことが、非常に大切なのであって、事実そういうふうにして、今日の自然科学は発達してきているのである。これは科学のすべての分野において行われていることである。ここではまずその中の代表的な場合、すなわち科学における予言ということについて、少し考察をしてみよう。

ある方面で、いろいろな知識が得られたとき、それを綜合してみると、今までの一つ一つの知識では気がつかなかったことが、何か次の段階に予期される。そこでこういうことがあるはずだと予言ができ、それを実験でたしかめてみる。そして予言どおりに、ぴったり当ったとする。そうなれば何人といえども、その理論を信用せざるを得なくなる。こういう予言をして、それが後に実験によって確かめられた例はかなりあって、いわゆる科学の勝利として、あげられているわけである。

その非常によい例は、ニュートン力学において、既によく知られている。太陽のまわりに、地球やその他いろいろの遊星がまわっている。この遊星の運動は、万有引力、すなわち距離の二乗に逆比例し、二物体の質量の積に正比例する引力に起因しているというのが、ニュートン力学である。ところがこの万有引力の法則をつかって、実際に地球とか、木星とか、土星とかいうものの運動を計算してみると、少しずつ狂っているのである。この計算は、万有引力が太陽と地球との間、太陽と土星との間というふうに、二体間に働くものとしてやってある。ほんとうは、そのほかに、太陽にくらべれば非常に弱い力ではあるが、遊星同士の間にも万有引力がはたらく。その影響を計算して、補正をすると、遊星の運動がもっとくわしく出せる。

そういう計算をくわしくやっていくと、だんだんよく合ってくるのであるが、それでも当時太陽から一番遠い遊星と思われていた天王星の運動は、どうしても計算と合わない。それで天王星よりももっと向うに、今まで知られていなかった遊星があるのかもしれないと考えた。そしてもしそんな遊星があって、その影響のために、この狂いが出たとすると、どういう距離のところに、どういう遊星があればよいかということが計算できる。こういう計算をして、何月何日の何時何分に、どの方向に望遠鏡を向けていたならば、そこにその遊星が見えるはずだという予言をした。そしてそのとおりにやってみたら、はたしてそういう遊星が見つかったのである。これが海王星である。この海王星の発見は、ニュートン力学の非常に力強いサポートになった。こういう予言は、万有引力の理論の力を借りなくては、とうていできない。この予言が、的中したということは、この理論の何よりも強いサポートである。そこでニュートンの力学が、非常な勢いで、物理学全般に強い影響を及ぼすことになった。

しかしその後だんだん観測が精密になっていくに従って、遊星同士の影響を非常にくわしく調べてみても、やはり実測とは少し狂いがあることが分った。そのうちで有名なのは、太陽に一番近い水星の運動である。水星の軌道は、その近日点が、百年間に、角度にして五七四秒移動することが観測によって知られている。遊星同士の影響を、万有引力理論によって計算すると、五三四秒と出る。その差は約四〇秒であって、これはどうしてもその原因がわからなかった。ところがアインシュタインの相対性原理による万有引力論では、この四〇秒の狂いが、ほぼ完全に説明できたのである。

これが相対性原理の一つの強いサポートになった。これだけでもたいへんなことなのであるが、更にアインシュタインの理論が正しいとすると、太陽の附近を通ってくる光線は、重力の場の影響を受けて曲るはずだという結論がでてくる。その予言をアインシュタインがしたのである。それまでは、光が真空の空間を通るときに曲るなどということは、夢にも考えられなかったことであるから、全く新しいことを予言したわけである。それをたしかめるために、英国の日蝕班が、エジプトの日蝕のときに出かけていって、きわめて精密な観測をしてみた。そしたらはたしてアインシュタインの予言どおりに、星が少しずれて写真にうつった。光線が曲れば星の位置が少しずれて見えるわけである。これも予言が実際に的中したみごとな例として有名である。

そのほか湯川博士の中間子の理論が出て、あとでアメリカで、その中間子が霧函の中で発見されたという例もある。あるいは電子はマイナスの電気を持っているものと思い込んでいたのであるが、ディラックの理論で、陽電子すなわちプラスの電気を持った電子もあるはずだということが、理論的に出された。その理論が出た頃は、たいていの人は、夢のような話と思っていたのであるが、後にアンダーソンによって、霧函の中で、この陽電子が発見された。これらはいずれも非常にみごとな例として、科学の歴史の上に残っている。

ところで以上述べたような例の外に、ここで少しくわしく説明しておきたいのは、マックスウェルによる電波の予言である。理論が実験の結果をいかに活かして、われわれの知識を広めていくかということを示す、もっとも良い例と思われるからである。

今日の文明は電気の文明である。ギリシャ時代から今日まで、人類がいろいろなものを発見してきたが、前世紀から今世紀にかけて、革命的に知識が進歩したのは、けっきょく電気が使えるようになったからである。電気がなかったら、今日の原子力など、もちろん出てこないし、われわれの日常生活も全く別のものになっていたにちがいない。電気はほとんど完全に、われわれの生活を支配している。その電気の中でも、電波の問題は、非常に大きな問題であって、マスコミを通じて、人間の精神生活までも左右しようとしている。電波というものが、今日の文明の大きな特徴であるといっても、過言ではない。この電波の存在、すなわち電気及び磁気の場は、真空の中を波となって遠くまで伝わっていくものだということを予言したのが、マックスウェルなのである。この予言には、数学がみごとに使われているばかりではなく、いろいろな知識を綜合するのに、理論がいかに有力なものであるかを示した非常によい例なのである。

われわれは、今日では電磁気という言葉を使っていて、電気と磁気とを別のものとしては取り扱っていない。たとえば電波といっているが、くわしくいえばあれは電磁波なのであって、電気の場の波と、磁気の場の波とが、空間を伝わっていく現象である。電気と磁気とは、空間のゆがみの両面であって、時間的変化がある場合には、両者は常に伴っている。しかし時間的変化がない場合は、両者は別々にあらわれてくるのであって、電気というものは、琥珀を猫の皮でこすったときにでてくるものである。これははっきりいえば、静電気の現象である。磁気の方は、磁鉄鉱と呼ばれている鉱石が、互いに相手を引っぱったり、はね合ったり、あるいは他の鉄片を引きつけたりする現象である。それで時間的変化がない場合は、電気と磁気とは、全く別の現象としてあらわれる。それで磁鉄鉱の性質を知らなくても、静電気は今日と同じように発達できる学問である。また猫の皮のことを知らなくても、磁気の学問は今日と同じものができ上ってよいはずである。ところが十九世紀のはじめになって、電気と磁気との間につながりがあるということが発見された。それはあまり有名ではないが、デンマークの物理学者エールステッドの発見であって、これは科学の歴史の上で大きな意味をもつものである。

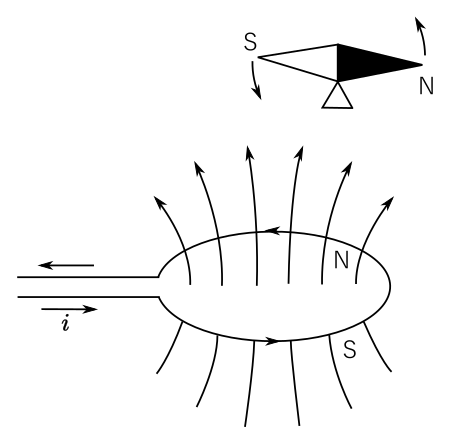
エールステッドは、針金で小さい輪（ループ）をつくり、その輪に電流を通しておいて、その輪の近くに、磁石の針を持っていってみた。すると針が動くということを発見したのである。磁石を動かす力は磁気であるから、電流が通っている針金は、磁石と同じ性質をもっているということが発見されたのである。実験は非常に簡単であって、第14図に示すとおりである。それでは電流の通っている小さい針金の輪は、どういう磁石に相当するかというに、第14図の方向に電流を通すと、このループの上の面が南極Ｓになり、下の面が北極Ｎになる。もちろん電流の方向を逆にすると、ＮとＳとは反対になる。こういうひらべったい磁石と同じ磁場を、その周囲に与えるのである。その磁場の強さは、流す電流の強さに比例する。これがエールステッドの法則といわれているもので、電気と磁気との間に、はじめて連絡をつけた発見である。

ここで問題になるのは、磁場の強さは、流れる電流に比例するという、その比例定数である。磁場の強さは磁気のクーロムの法則から単位がきまり、電流の強さは、電気のクーロムの法則から単位がきまる。それで比例式の両側を、それぞれの単位ではかって、数値にしてしまうと、比例定数が数値で出てくる。実際に実験によってこの数値を出してみると、ｃｇｓ単位では、1/3×10¹⁰という値になる。3×10¹⁰は真空中の光の速度に出てくる数値で、これはｃであらわすことになっている。それで比例定数はである。これが後に電磁波の伝播速度になるのであるが、ここでは単に磁気と電気との関係式に出てくる比例定数である。

以上は電流を通すと、周囲に磁場ができるというのであるが、それならば、磁場を何とかすると、電気が起きはしないか、すなわちこれと逆の現象がありそうなものだと考えたのが、ファラデーである。

ファラデーは磁場の中に針金のループを置いて、このループを電量計につないだ。第15図に示したような簡単な装置である。この中で、電量計というのは電解槽のことであって、硝酸銀の水溶液の中に、プラスとマイナスの電極板を入れたものである。硝酸銀は溶液の中では正の電気をもった銀イオンAg⁺と負の電気をもった硝酸銀イオンNO₃^-とに分離している。電圧がかかると、銀イオンは陰電極について銀めっきになり、硝酸銀イオンが陽電極にくっつく。このイオンの移動が、電解槽中の電流であって、これは針金を通っている電流ｉと同じ値である。

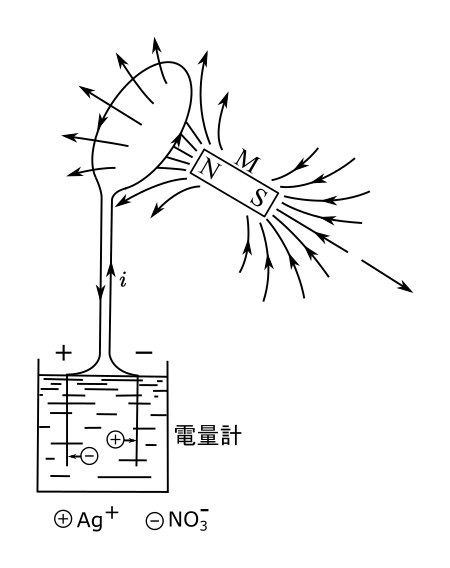
この電量計は、電流をはかるためのものではなく、ある時間内に通った全電量をはかる装置である。銀イオンの帯電量ｅはわかっているので、陰極板にくっついた銀の目方をはかれば、流れた全電量が計算される。電流ｉが一定のときは電流計でｉをはかって、それに時間をかけたものが、流れた全電量になる。しかしｉが時間的に急激に変化する場合は、電流計ではかれない。しかしこの電量計ならば銀の目方をはかればよいので、どんなに途中で電流が変化していても、全電量がはかれる。

このままでは、電池も何もないのであるから、電流は流れず、銀もくっつかない。しかしこの時に、磁石を動かして、磁場の強さを変化させてやると、針金の中に電気が流れることがわかった。これがファラデーの感応電気の発見である。そのときに生ずる電流の強さは、針金のループの中を通っている磁力線に関係するが、その数ではきまらないのであって、磁力線が時間的に変化する割合に比例するのである。磁力線は磁場の強さをあらわすもので、この数が多いほど磁場が強いことを示している。強い磁場があっても、電気は流れない。磁場の時間的変化が速いと、強い電流が流れるのである。たとえば、第15図の装置で、磁石Ｍを急激に遠のけたとする。するとループの中を通っている磁力線が急激になくなる。そのなくなる割合に比例して、図の矢印の方向に電流が流れるのであるが、厄介なことには、変化の割合に比例するので、非常に短時間のうちに磁場がなくなれば、非常に大きい電流が流れる。ただし電流の継続時間は、その短い時間のうちだけである。磁場がなくなりつつある間、そのなくなり方は一定ではないので、電流も短時間内に激しく変化し、電流計にはとてもあらわれない。しかしその電流を積分した値、すなわち流れた全電量は、電量計ではかることが容易である。電量計を使ったのは、変化しつつある時間内の積分した値をはかるためである。それで電量計を用いると、電流の強さが、磁場の変化の割合に比例するという、その比例定数を実験的にきめることができる。実際にはかってみると、この比例定数の値は、前の場合と同じく、という値である。

電気と磁気との間の関係について分った実験的事実としては、この二つだけである。ところがこの二つのことがらから、マックスウェルは、電気及び磁気の場というものは、光と同じ速度で、波となって空間をつたわっていくべきものだということを、理論的に導き出したのである。しかも驚くべきことには、そのときの電波の波は、比例定数ｃの値、すなわち、3×10¹⁰糎/秒の速度で伝播するということまで、理論的に出てきたのである。光も実は電磁波の一種であって、ただ波長がひどく短いだけのちがいである。それで電磁波と光とが、同じ速度で伝わるのが当然なのであるが、そういうことは、後になって、わかったことである。電気と磁気との測定から、光の速度の数字3×10¹⁰というような数値が出てくるということは、いかにも不思議なように見える。しかし本当は、不思議ではないのであって、光も電磁波であるから、その数値が、電磁間の関係式の中に出てきても、ちっともおかしくはないのである。ただし、磁場の強さが電流に比例し、その比例定数はであるという式と、感応電流の強さが、磁力線の数の時間的減少の割合に比例し、その比例定数がであるという式とを、いくらにらめていても、このｃが電磁波の伝播速度であるということはわからない。それをマックスウェルが、理論的に導き出したのである。

エールステッドの発見とファラデーの感応電気の発見という二つの事実から、理論の力によって、電磁の場が波になって伝わるということが、どうして出てきたか。こういう場合には、たいていやり方がきまっているのである。まずこの二つの法則を、式の形にして表わす。これが最初にやることである。今の例では、電流の強さと、それが生ずる磁場の強さとの間の関係が、実験でわかったわけであるが、そのとおりを式に書く。比例する場合ならば、比例定数を入れれば、等式になる。そういう式を二つ作っておく。第1表にあげた（１）（２）の二つの式がそれである。しかしこれらの式は、与えられたループについてあてはまる式であるから、実際の計算は、ループがちがえば、みなちがった計算をしなければならない。こういう式は、数学では積分型の式といわれている。ところが積分型の式は、単なる数式の転換によって、微分型になおすことができる。微分型の式というのは、非常に小さい部分についてあてはまる式である。この式は、微分の形で、どういう法則が成り立つかを示すものである。それでエールステッドの法則（１）式は単なる数式の転換で第1表の（３）式になる。次ぎにファラデーの法則（２）式を、微分型の式になおすのであるが、エールステッドの方は、磁場の強さを電流の函数とした関係であり、ファラデーの方は、（２）式に見られるように、電流を磁場の変化の函数とした関係である。一方は磁場で、一方は電流であるから、対称的な形にするためには、電流を電場になおしたい。ところがちょうどよい工合に、オームの法則というのがあって、電流は電圧に比例することがわかっている。電圧というのは、電場の一つの変形であるから、オームの法則を微分型になおして、（２）式の転換の途中に入れる。そうすると、電場と磁場の変化との関係式、第1表の（４）式が得られる。（３）式と（４）式とは、内容的には、（１）式（２）式とそれぞれ同じもので、単なる数式の転換とオームの法則の導入とによって得られた式である。（３）式及び（４）式中のｃは、（１）（２）式からみたもので、前のとおり3×10¹⁰の数値である。

ところでこの二つの式を並べてみると、ここに当然予期されるような仮定がほしくなってくる。というのは、式が二つのところに、変数がＨ・Ｅ・ｉと三つあっては困るので、これを二つにしたいからである。その仮定の一つは、電場の変化は、電流の一種とみられるから、電場の変化にも、エールステッドの法則が適用されて、磁気作用が生ずるとする仮定である。今一つはオームの法則は、定常電流について実験的に知られた法則であるが、電流が非常に速く変化する場合にも、そのままの形で適用されると仮定する。

その二つの仮定を入れて、真空中の場合について、さっきの二つの式を、単なる数式の転換によって、どんどん式の形を変えていく。すると最後は、第1表（５）（６）の式が得られる。この二式の中でというのは、ｘ、ｙ、ｚでそれぞれ二度微分して足すということを示す記号である。

すなわちこの二式とも、時間で二度微分したものが、空間的に二度微分したものに比例し、その比例定数はであることを示している。ところがそういう式は、波の伝播の式であり、その伝播速度は、比例定数の平方根であることが、微分方程式の方で、前からよく知られている。それで（５）（６）の両式を普通の言葉に翻訳すれば、電場も磁場もｃの速度で、伝播するということになる。マックスウェルは、この最後の式に到達したので、電磁波の存在を予言したのである。

ところが、その後ヘルツによって、実際にそういう電波が存在することが発見された。そして今日のラジオ、テレビにまで発展したのである。また一方電磁波の速度が光の速度とひとしいことから、光も電磁波の一種であろうと考え、それが確認されて、今日では、光学は電磁光学として、電磁気学の一部門になったわけである。

前に数学というものは、人間の頭の中で作られたもので、人間の知らないことは、数学では出てこないということをいった。ところが光が電磁現象であることを知らなかったのに、という式が、それを教えてくれたのは、前の説と矛盾していないかといわれるかもしれない。しかしそうではないので、この式は電磁波がｃの速度で伝わるということだけを教えているのである。ただ電磁波の速度と光の速度とがひとしいことが分ったので、光も電磁波の一種らしいという示唆を得て、それではというので、今までに知られている光の性質の一つの屈折率を検討してみたら、はたして光も電磁波であるということがわかったのである。

それにしても、電気および磁気の場が、ｃの速度で伝播していくことを、数式が教えてくれたことは、まことに驚くべきことである。ところがこの数式は内容的には、エールステッドの法則と、ファラデーの法則、すなわち（１）式及び（２）式とほぼ同じものである。ただ仮定が少し加わっただけで、本質的には、そうちがわない。そうすると、電磁波の存在は、エールステッドの法則と、ファラデーの法則との間に隠されていたことになる。しかしどんな大天才でも、この二つの法則の中から、電場、磁場は、空間を波となって伝わっていくものだということを、かぎ出すことは不可能であろう。それは、マックスウェルほどの頭脳をもってして、数式によって展開してみて、はじめてわかったことである。数学というものが、人間の頭の中で作られたものではあるが、それは個人の頭脳でつくられたものではない。たくさんの数学者の頭脳で作られたものであって、いわば人類の頭脳がつくったものである。そういう一種の超人であるところの数学の力を借りて、はじめてエールステッドとファラデーとの二つの法則から、電波の存在が予言できたのである。

すなわち理論がその価値を発揮する場合は、この例のように、知識を整理することによって、普通の人間の考え及ばないところまで、思考が深められ、それによって新しい知識が得られ、次の発展を促すという場合である。ここまでいって、はじめて理論が、ほんとうの価値を発揮するのである。