科学における人間的要素

今までの話のしめくくりとして、「科学における人間的要素」という問題を考えてみよう。

科学における人間的要素というのは、それ自身の中で矛盾している言葉のように聞えるかもしれない。自然科学というものは、自然界にある真理を研究する学問であって、この真理は、人間などとは無関係に存在するものである、と一般に考えられているからである。一面においては、そのとおりなのであるが、今までたびたびいってきたように、人間を離れて自然というものはないという考え方もできるのである。もちろん人間が一人もいなくても、地球は存在しているであろうが、われわれが見ている自然は、なくなるであろう。人間をはなれて存在している自然の中から、いろいろな法則を引き出したり、実態を見きわめたりするものは人間なのであるから、われわれが現在もっている自然像は、人間を離れては存在しないものである。

その上一口に自然像とはいうものの、自然像をつくるについての問題の出し方が、場合によっていろいろちがっている。

前に「生命の科学と物質の科学」のところで、説明したように、生命と物質とでは、現在の科学は、その取り扱い方をちがえている。すなわち問題の出し方がちがっている場合が多い。前にもあげた例であるが、人間の寿命というような、非常に複雑なものでも、一つの国の国民全体というような大ぜいの人間については、その寿命に簡単な法則があてはまる。一方電子の流れなどは、磁場と電場との強さが与えられれば、正確に計算できるといわれているが、これとても、その流れの中の電子一つ一つの実際の運動はわからない。それで、ある現象がわかるとかわからないとかいうことは、問題の出し方いかんによるところが大きい。問題を出すのはもちろん人間であるから、ここに人間的要素が科学の中に深くはいりこんでいるわけである。

最近の物理学や化学の例を見ると、これらの学問の進路は、原子論の方に向いている。物質をこまかくわけて見ていくと、最後の姿は原子であるという時代があった。その原子が、次ぎには原子核と電子とからなっていることになり、その原子核がまたいろいろな素粒子からなっているというふうに進んできた。すなわち物質の構成要素の中へ中へと目を向けていく。この半世紀間は、そういう方向に、学問が発展してきたのである。しかしこれが物理学におけるただ一つの方向ではないのである。

前世紀の後半には、いわゆる熱力学的な研究のやり方が、非常に盛んであった時代がある。熱力学でも、流体力学でも、ファラデーやマックスウェルの電磁気学でも、物質を分子的に見ないで、全体として取り扱っているので、物理学の方では、これをマクロスコピック（巨視的）なものの見方といっている。これに反して、原子論的な見方は、ミクロスコピック（微視的）といわれている。巨視的な見かたでも、もちろん科学は成り立つので、十九世紀の科学の進歩は、巨視的の立場をとった物理学の勝利に帰するところが多い。十九世紀は巨視的であったが、二十世紀にはいって、微視的になったというと、巨視的が初歩で、微視的が更に発達した見方というふうに思われるかもしれない。しかしそうではなく、この見方のちがいは、問題の種類によるのである。たとえば十九世紀後半から今世紀の初めにかけて、気体分子論の研究が一時大いに流行ったことがあった。気体を小さい硬い球の集合と見なして、すなわち気体を微視的に取り扱って、いろいろな性質を説明しようという試みである。この学問もかなり進歩したが、巨視的に取り扱った熱力学の方が、ずっと成果をあげた。要するに問題によるのである。

流体力学なども、空気の分子のことは考えず、空気を全体として取り扱う巨視的な見方で進歩した学問である。今日音速の何倍という速い飛行機が飛んでいるが、これは流星以外には地球上になかったことを、人工で可能にしたので、たいへんなことである。しかし飛行機が飛んでいるとき、空気の分子の一つ一つがどういうふうになっているかというようなことは、何もわかっていない。そういうことを知らなくても、あの飛行機の設計ができるのであるから、知る必要がないのである。この頃世界を騒がせている人工衛星なども、原子論が発達したためにできたものではない。自動調節器の一部には、そういうものも使われているかもしれないが、大部分の問題は、巨視的な科学の問題である。将来原子力エンジンができれば、もっと性能がよくなるであろうが、それは次ぎの問題である。

それで、物質の内部へ、内部へと見ていくことだけが、科学の本質ではないのであって、いろいろな方向に、科学は進歩していくのである。ただある方向に科学が向ったときに、何か非常に面白いことが見つかり、その方向に進めば、重要な発見がありそうに思われると、大ぜいの人がどんどん集ってきて、その方向へ科学が大いに発展する。これは外観だけ見ると、美術などの場合とちょっとにている。ある流派の絵に人気が出てくると、みなその方向に集中して、その流派が盛んになるのと似たところがある。もちろん科学の場合は少し違うが、人間が科学をやっている以上、両方に似ているところがあるのは当然である。

ところで原子論的な方向に、人間の眼がむいて、そういう面の研究が進み出したのは、前世紀の終りごろからである。電子やイオンの存在が確認され、一方放射能元素が見つかって、ギリシャ以来物質の窮極の姿と思われていた原子がこわれて、いろいろなものが飛び出すという全く新しい知識が得られた。それでこれは非常に重要なことであるというので、その方向にどんどん研究が集中して、原子論という今日の科学の方向が決定されたのである。

ところで、原子論でまず取り扱うのは、一つの原子について、その構造とか性質とかを、見るわけである。物質は非常に多くの原子からできているが、何億という原子を、一ぺんに調べてみることはできない。それでまず一つの原子について、その中にどういう原子核があって、電子がその周囲にどういうふうに存在しているかという研究をする。それから原子核がどういう構造や性質をもっているかというふうに、研究を進めていく。しかし、一つの原子について、その構造がすっかり分ったとしても、その原子が非常にたくさん集ってできている物質の性質が、それですっかり分るかというと、そうはいかないのである。というのは原子一つが示す性質は、普通の場合非常に微弱なものであって、測定にはかからない。ただそういう原子が非常にたくさんあった場合、その全体がどういう性質を現わすかということは、実験にかかる。すなわちわれわれの認識にかかるわけである。それで一つの原子の性質がわかっただけでは足りないので、そういう原子がたくさん集ったときの性質がわからなければ、実験にかけてみることができない。すなわち理論が合っているかどうかを、確かめてみることが、できないわけである。ここに統計、すなわちたくさんのものが集ったときの全体としての性質という問題が、はいってくるわけである。そういう意味では、原子論という学問は、統計の学問であるともいえる。少なくとも半分は統計の学問である。

ところで統計というものは、数が非常にたくさんある場合にのみ用いられる方法である。一つ一つの要素は、それぞれちがった特性をもっていても、全体として見ると、それらの特性は互いに打ち消して、ある法則が、確からしさという形で出てくる。そしてその確からしさの程度は、数が多いほど増してくる。

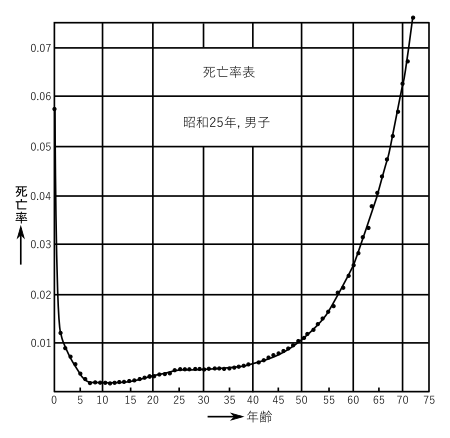
第16図は昭和二十五年の資料による日本の男子の死亡率表であるが、これを見ると、年齢と死亡率との間には、はっきりした関係があることがよくわかる。死亡率というのは、ある年齢の人が、向う一年間にどれくらい死ぬかという率であって、五十歳の人は、曲線からみると、〇・〇一一になっている。すなわち五十歳の人は、一万人中の百十人が向う一年間のうちに死ぬのである。生れてはじめの一年間は死亡率が高く、十歳くらいの頃が一番低い。そして壮年の頃に一定の値がつづき、五十歳以上になると、また高くなる。七十歳になると、向う一年間に一万人中六百二十人くらい死ぬ。年齢と死亡率との関係は、滑かな曲線になるので、そのうちのいくつかの資料が欠けていても、曲線の形からその値を出すことができる。これでみると、人間の寿命などというものも、案外簡単にわかるものである。しかしこれは数が非常に大きいときに、こういう関係が出てくるので、数百人や数千人の人間について調べたのでは、点はばらばらに出てきて、簡単な法則はとても見つからない。

もっとも、ここで出てくる法則というのは、全体としてみたときの確からしさであって、個々の人間にとっては、この法則はあてはまらない。平均寿命は、五十八歳でも、生れてすぐ死ぬ子供もある。そういう子供の親にとっては、平均寿命が五十歳でも、八十歳でも、どうでもよいので、そんな知識はあってもなくてもよい。しかし一方保険会社にとっては、この平均寿命の知識は、大いに役に立つ。この場合、個人個人の寿命を論ずるのは、この問題を微視的に見ているので、国民全体についてその平均寿命を調べるのは、巨視的に見ているのである。そしてたいていの場合、科学の実証的な結果は、巨視的に問題を取り扱ったときに出てくる。

これは生命現象がはいっている問題の場合だけに限らない。生命のない物質の科学でも同じことである。その例として、放射能元素の崩壊の問題をとりあげてみよう。ラジウムがその代表であるが、いわゆる放射能元素は、原子の内部にある原子核が、自分で放射線を出して自然崩壊をする。放射線には、α（アルファ）線、β（ベータ）線、γ（ガンマ）線の三種類あって、そのうちの一つ乃至三つを出す。そして放射線を出したあとのその原子は、他の元素の原子になる。第2表にラジウム系の放射能元素の系列の一部を示してある。ウランから、いろいろな段階を経て、非常に長い年月かかって、ラジウムができる。ところでこのラジウムの原子は、α、γの二種の放射線を出して、ラドン（ラジウム・エマナチオン）にかわる。このラドンの原子は、α線を出して、ラジウムＡという別の元素の原子にかわる。この原子がまたα線を出して、ラジウムＢの原子になり、以下Ｃ、C'を経て、鉛の同位元素であるラジウムＤにかわる。これは放射能をもった鉛で、更に崩壊して、最後は普通の鉛になる。

ところで崩壊の速度であるが、それは元素によってみなちがい、たとえばラジウムなどはゆっくり崩壊するが、ラジウムＡは、みるみるうちに崩壊してしまう。崩壊の速度は、単位時間中に、全原子の何割が崩壊するかできめる。すなわち原子の死亡率（崩壊定数）が、崩壊速度であって、これをλ（ラムダ）であらわすことになっている。死亡率がわかれば、どれだけの時間がかかると、生き残った原子の数が、はじめの原子数の半分になるかが、計算できる。この時間を半減期といい、Ｔであらわすことになっている。半減期が短いほど、はやく崩壊するわけである。Ｔとλとは、第2表に示してあるが、たとえばＴを見ると、ラジウムは一六二二年、ラドンは三・八二五日、ラジウムＡは三・〇五分というように、ひどくちがう。ラジウムC'のように、〇・〇〇〇一六四秒とういような、極端に短いものもある。

原子の死亡率λの方が分り易いが、ラドンでλ=1.26×10^-4/分とあるのは、現在から向う一分間内に、一万個の原子のうち一・二六個の割合で原子が死ぬことを意味している。百万個中一二六個といってもいい。ところがラジウムＡの原子の死亡率は、一分間内に、一万個中二三一〇個の割合、ラジウムＢでは、一万個中二五九個である。ここでは死亡率といったが、これは同時に出生率でもある。死んだラドンの原子は、ラジウムＡの原子になるので、ラドンの死亡率は、ラジウムＡの出生率でもある。それで一つの元素に注目してみると、ある出生率で生れながら、ある死亡率で死んでいる。それで定常状態では、一系の放射能元素の存在量の割合がきまっていることになる。たとえばラジウムＡについてみると、親であるラドンから、一分間に、一万個について一・二六個の割合で、新しい原子が供給され、同じ時間内に、現在ある原子のうち、一万個について二三一〇個の割合の分がなくなっていく。一万個について一・二六個の割合で供給され、二三一〇個の割合でなくなったら、すぐマイナスになってしまいはしないかという心配はない。ここでいっている数字は、割合をいっているのである。ラドンがたくさんあり、ラジウムＡが少ししかなければ、出生と死亡とがつり合って、一定量に保たれる。

ここで重要なことは、原子の出生率あるいは死亡率はわかっているが、どの原子が死ぬかということは、全然わからないという点である。ラジウムＡについていえば、ラドンからどんどん原子が供給しつづけられているので、現在いる原子の中には、大分前にできたものもあれば、瞬間前にできたものもある。老幼さまざまの原子がまじっているが、それらをひっくるめて、一分間に、一万個について二三一〇個の割合で死んでいる、ということだけしかわからない。人間の死亡率にしてみたら、国民全体の平均寿命しかわかっていないことになる。第16図に見られるように、年齢別に死亡率がどうちがうかというようなことは、原子の場合は全然わかっていないのである。こういうふうに見ると、物質の科学は対象が比較的簡単であるから、研究し易い、生命の科学は、非常に複雑であるからわからないことが多い、というようなことは、簡単にはいえないことになる。少くも人間の寿命の方が、放射能元素の原子の寿命よりは、よくわかっている。それだのに一般には、なぜ人間の寿命の方がわからないように、思われているかというに、それは統計の中の個を求めるという無理な注文をしているからである。統計ではあくまでも、確からしさを取り扱っているので、個々の問題にはふれない。人間の寿命の問題などが、そのよい例である。ある人は非常に長生きをする。ある人は自動車事故で死ぬというふうに、人々によってその寿命はいちじるしくちがうが、非常にたくさんの人数について統計をとってみると、あるきまった法則が出てくるのである。原子論の方では、原子一つ一つの性質を調べているが、最後のところで、われわれの認識にもってくるときには、たくさんの原子のあつまりについて、統計的に結果を見ているのである。

それで原子一つの場合と、原子が何億何兆と集った場合と、この両方についての知識を得ているわけである。要するにこの両極端の場合だけに問題が解けるので、そこだけを取り扱っている。ここに人間的な要素がはいっているのである。数が非常に少いときには、力学的方法が見える。また非常に多い場合は、統計的方法が応用できる。

困るのは、中途半端な場合である。古典力学の方がわかり易いので、その例をあげると、万有引力のような基本的なそして比較的簡単な形の法則ですら、問題が精密に解けるのは、二体運動の場合だけである。地球が楕円の軌道を描いて、太陽のまわりを廻っているというような場合だけに、問題が解けるのである。実は地球と太陽とを一つの系とみた場合、その重心を中心として、地球も楕円軌道で廻り、太陽も楕円軌道をとる。しかしその重心は、太陽の中心に近いところにあるので、太陽がとまっていて、地球がそのまわりを廻っていると考えても、普通の計算にはそれで間に合う。この計算ならば、ちゃんとできる。しかし、もう一つ星があって、三つの天体間に、互いに万有引力が働いている場合の運動となると、これは昔から三体運動と呼ばれて、解けない問題になっている。ただ一つの星の影響が、ごく弱いときは、二体問題に補正項が加わるという形で、近似的に解ける。前にいった海王星の発見なども、この近似解をかさねていってできたのである。三体問題でさえ解けないのであるから、四つ、五つとなったら、とうてい解けない。

しかし気体分子論のように、気体を何億何兆という硬い小球が集ったものと見る場合は、またこれを解くことができるのである。しかし気体粒子が、五十とか百とかいう場合には、今のところ問題解法の手がかりがない。一つの性質もわかり、うんとたくさんある場合の性質もわかる。その中間は現在の科学では抜けている場所である。しかし現在の科学の成果は、非常に華々しいものであって、原子力が解放されたり、超音速のジェット飛行機ができたり、人工衛星がとんだりしているのを見ると、人間的要素などというものから、とっくに脱却しているように見える。自然界には、ほんとうの法則が埋れていて、宝探しをしている人間が、いろいろ探しているうちに、そのものずばりにぶつかって、それをつかまえたというふうに、考えてもよさそうにも思われる。しかしよく考えてみると、ほんとうはそうではないのである。

こういうことを論ずる場合、一番大きな問題は、一体自然界に法則というものがあるかないかという点である。今までの考え方では、法則があるということは、証明できることではないので、法則があると仮定して組立てたものが科学なのである。もっともそういう仮定のもとに組立てた科学が、今日のように発展し、つぎつぎと自然に対する新しい知識が得られているという意味では、法則が実際に存在しているといってもよい。しかしたびたびいったように、自然界から現在の科学に適した面を抜き出して、法則をつくっているのである。ということは、かつて万古不易の法則というものは、あったためしがないからである。今までに一番重要で確固たる法則といえば、物質不滅の法則とエネルギー不滅の法則とであった。この二つの法則が、物理学の二大法則であって、この基礎の上に立って、今日の科学が組立てられてきたのである。いろいろな法則が今までにあって、互いの間に対立があったり、反対論があったりしてきたが、この二つの法則だけは、近年までだれも疑う人がなかった。これこそ万古不易の法則と誰もが考え、この上に立ってはじめて科学が成り立つものと考えられていた。

ところが第四章でくわしく述べたように、二つの法則も、そのままの形では存在し得ないことが、原子論の発達によって、近年は常識となったのである。それをなぜ昔は万古不易の法則と思っていたかというに、世界中だれがどこで、どんな精密な実験をしてみても、また物質の姿をどんなに変えてみても、その質量は変らない。そういうことが実験的にたしかめられていた。エネルギーの方も、くわしく実験してみると、なくなったように見えても、熱になって逃げるとか、輻射線になって逃げるとかしたのであって、それを全部ひっくるめると、エネルギーが恒存されることが、実験的に証明されたと思っていたからである。

ところが実際はそうでなかったのである。実験的に証明されたとはいうものの、ほんとうはいつでも少しはちがっていたのである。しかしそれが実験の誤差の範囲内ならば、それでよいとしていた。あるところまでは、実験の精度の範囲内でわかる。その先は、実験の誤差である。誤差の範囲内で一致するのだから、これは一致しているといっていたわけである。誤差の範囲内だから、よろしいというのは、法則の方を先に仮定していたのである。何か不変なものがないと、論理の足場がないので、物質不滅とか、エネルギー不滅とかいう足場をつくった。今日物質とエネルギーとが互いに転換できるということになっても、その和は不変とするのであって、そういうわくを作っておいて、それによって自然界を見ていく。それでやはり人間的要素はいつまでも附随していることになる。

以上は、いわば高級な意味での、科学における人間的要素の話であるが、もっと卑近なところにも、人間的要素が、科学の中に、たくさんはいっている。まちがった論文とか、ごまかしの論文とかいうものは、もちろん人間的要素が強いものであるが、ここではそういう問題にはふれないことにする。そういうものでなしに、ちゃんとした相当立派な仕事の中にも、人間的要素が強くはいっていた例が、今までにたくさんあった。たとえば今日の原子核物理学の基礎となった同位元素の発見にも、その例が附随していた時代もある。

アストンが最初に同位元素を発見したときに、大勢の学者がこれに反対した。もし原子が整数で割り切れる目方のものであるとしたら、原子量が一定に出るのはおかしいではないかという議論である。

たとえば水素の原子量は一・〇〇八〇であり、塩素の原子量は三五・四五七というふうに、みな端数がついていて、その端数はきちんときまっている。各種の同位元素のまじったものとすると、その割合が、地球上どこで調べた元素でも、みな同じ割合になっているのはおかしいではないかという議論である。これに対してアストンは、それは地球の創成のはじめに、各種の同位元素が非常によくまじってしまったために、どこでも一定の原子量の元素がみられるのであるという説明をしていた。今日になって、いわゆる重水とか三重水素の水とかいうものが発見されてみると、何も地球上の水が同じ目方ではないことがわかった。手近かなところでもその例はいくらもあるので、たとえば普通の美しい形をした雪の結晶をとかした水は、普通の水より少し軽く、雲粒付の雪をとかした水は、少し重い。そういう水を分解してつくった水素の原子量をはかったら、ちがっているにちがいないのである。その後ほかの元素についても、同位元素のまじり方が少しちがう場合があることがわかり、同位元素の自然分離の研究が、一時流行ったことがある。以前から原子量の精密な測定は、ずっとつづけられていたので、少し原子量の違った値も出たことがあったにちがいない。しかし自然分離が知られなかった時代には、そういう測定は何かのまちがいあるいは実験誤差として、棄てられていたのではないかと思う。もしそうだったら、卑近な意味での人間的要素がはいっていたわけである。

今世紀のはじめ、ベックレルがウラン鉱石から放射線が出ることを発見し、ひきつづいて、キュリー夫人が、ラジウムを発見してから、一時たいていの金属から放射線が出るといって、騒がれたことがあった。銅貨を写真乾板の膜面の上に載せて、長い間暗室に放置しておいて、現像してみると、銅貨の模様が、はっきりと出てくるのである。いろいろ条件をかえて、実験をしてみても、いつでもこの像があらわれる。それでてっきり、銅から非常に吸収され易い放射線が出るものと考えた。空気を通るとすぐ吸収されるので、普通にはかったのでは出てこないが、写真の膜面の上にじかにおけば、検出されるのであろう。この放射線には、金属から出る放射線という意味で、金属線（メタル・レイ）という名前までつけられた。そしてちゃんとした物理の雑誌に、その論文も出ている。

しかしその後の研究によって、これはまちがいであったことが分った。極端に乾かした空気の中で、同じ実験をくり返してみると、像が現われないからである。けっきょく空気中の水蒸気から、銅の接触作用で、過酸化水素が微量にできて、それが化学的に、写真乾板に感光と同じ結果を生じたのであるという説明になった。

写真乾板に「感光」したといっても、化学的な原因によることも屡〻あり、必ずしも光線または放射線があたったためとは限らない。そういうことは、前からも分っていたのであるから、この「金属線事件」などは、ウランやラジウムにあおられた、一つの社会的現象と解されるであろう。

この事件などは、原因がわかったので、まだ始末がよい。これと似たような流行にあおられた研究で、本人は意識していないが、人間的要素のかちすぎた研究が、案外たくさんあるのではないかと思われる。

その一番大がかりのものは、約十年にわたって、世界中を騒がせた、ミトゲン線の研究である。それは生物線とも呼ばれ、生物の細胞が分裂するときに、一種の放射線を出し、この放射線が他の細胞にあたると、その細胞の分裂を促進する性質をもっている。はじめ玉葱の芽から、そういう放射線が出ることが「発見」され、その後いろいろな生命現象、たとえば酵母や動物の生きている血からもこの生物線が出るということになった。

もしほんとうにそういうものがあったら、これは生物学をひっくり返すような大事件である。それで世界中にわたって、大勢の医学者や生物学者が、この問題をつつき、専門雑誌に出た論文の数だけでも、三百篇くらいはあったであろう。立派な数百頁の単行本も、二、三冊出ている。ひょっとすると、医学博士も数人できているかもしれない。

全く新しい分野のことであるから、研究はどんどん進み、つぎつぎと新しい「事実」が見つかった。この線は、ガラスは通らないが、水晶なら通過する。それで水晶分光器で、スペクトルに分解することができる。生物の種類及び状態によって、その強度もまたスペクトルの配列もちがう。たとえば健康な人間の血と、癌にかかった人の血とは、ちがった生物線を出す、というような騒ぎにまでなった。

この生物線の研究は、世界中の相当な学者が、百人近くもかかって、約十年にわたって、着々と進められ、立派な単行本になるくらいの知識が得られたので、一時はその実在を誰も疑わなかった時代もある。しかし問題は検出器にあって、ほとんどの測定では、生物の細胞を検出器として使っていた。その細胞の分裂が促進されれば、生物線がそこへきたと判定するのである。これでは少し心もとないので、物理学者の方で、その検出法の研究が始められた。一番簡単なのは、写真乾板に感光するかどうかというのであるが、これはほとんど検出できなかった。たまにぼんやり黒ずんでも、玉葱から出る何かの蒸気の化学作用かもしれないので、決め手にはならない。

一番よいのは、ガイガー計数管であって、これならどんな弱い放射線でも検出できそうである。それでガイガー管を使った研究が、約十篇発表されたが、面白いことには、その半分が肯定的結果であり、半分が否定的結果に終った。それで生物学を書き換えるくらいの勢いであったこの大問題も、けっきょくは、正体不明のまま、いつの間にか、立ち消えになってしまった。この頃は、ミトゲン線のことなど、きいたこともない人も多いであろう。しかしこれは今から二十年くらい前の話であって、そう昔の話ではないのである。

生物からでる放射線で、生物でしか検出できないものがあっても、別に現在の科学とは矛盾しない。ジェームスの言葉を借りれば、科学は何が存在するかはいい得るが、何が存在しないかはいい得ない学問であるからである。それで生物線のようなものが、存在しないとはいわないが、少くとも二十年前の生物線ブーム時代の研究には、人間的要素が、そうとう強く働いていたとはいっていいであろう。

それから、最後に形の問題にちょっと触れておこう。これはまだ随筆科学論にもなっていない思想であって、本文では深入りをしない。興味のある方は、附録の「茶碗の曲線」を参照されたい。ただ一つ注意すべきことは、今日の科学は数学を使う関係上、量の科学にいちじるしく傾いているという点である。形も科学の対象になり得るものであるが、今日の科学の中には、形の問題はほとんどはいっていない。「茶碗の曲線」にくわしく書いてあるように、梅の枝ぶりと桜の枝ぶりとは、葉がなくても、一目見ればわかる。しかしその差を量的にあらわそうとすると、なかなかむつかしい。実際に枝わかれの角度を、各種についてみなはかり、つぎの枝までの長さをみなはかって、統計をとってみても、その差は出てこないであろう。梅の木にも、いろいろな梅の木があり、桜にも、いろいろな桜がある。それで数字の上では同じような分布をしていて、梅には梅の形、桜には桜の形があっても、ちっともおかしくはない。分析しても差が出なくて、全体としてみたときに、梅の木か桜の木かということが一目で見分けられる。そういう性質の問題は、今日の科学の中には、採り上げられていないのである。少くとも、路傍におかれている問題である。

自然科学がこのごろ非常に長足の進歩をしたために、科学万能的な傾向が、風潮になりつつあるように思われる。しかし自然科学は、人間が自然の中から、現在の科学の方法によって、抜き出した自然像である。自然そのものは、もっと複雑でかつ深いものである。従って自然科学の将来は、まだまだ永久に発展していくべき性質のものであろう。