測定の精度

今日では、物理学が、科学全般にわたって、その基礎になっていると、一般に思われている。ところがその物理学のさらに基礎をなしているものは、測定である。測定によって、自然現象の中から、量的の性質を抜き出し、その性質自身、または各量的性質の間の関係をしらべるのが、一番基本的な科学の方法である。

ところでここに一つ非常に大切なことがある。それは測定には必ず誤差がともなっているもので、いかなる方法を用いても、われわれは自然の本当の値を知ることはできない。測定によって得られる結果は、常に近似的の価である。これは測定が下手であるとか、機械が不正確であるとかいう問題ではなく、本質的な問題なのである。測定の内で、一番簡単なのは、長さの測定であるが、今あるものの長さを測る場合、一センチメートル目盛の物差で測れば、何メートル何十何センチというところまでは測れるが、センチメートル以下の所は分らない。一ミリ目盛の物差で測れば、ミリメートルの桁までは出せるが、それ以下は分らない。更に顕微鏡を使えば、千分の一ミリまで測れるが、その下は測れない。電子顕微鏡を使って、たとえ十万分の一ミリまで測っても、それよし以下はどうしても測れない。どんなに科学が進歩し、機械が発達しても、だんだん測定の精度が増すだけであって、ほんとうの値というものは、永久に分らない。もっとも人間が自然を見ているのであるから、人間が見得るところまでしか見られないのは、当然な話である。

測定し得る精度のさきを、物理学では、誤差といっている。それで誤差といっても、何もまちがいという意味ではなく、測定の精度の範囲外という意味である。そしてある法則がほんとうか、まちがっているかを、実験でたしかめる場合には、誤差の範囲内で合っていれば、それをほんとうというのである。誤差はもちろん小さいほどよいが、物理学で「精密な測定」というのは、誤差の絶対値の大小をいっているのではなく、測定値と誤差の比率が小さいほど、それを精密といっているのである。たとえば、大きさ百分の一ミリのばい菌の顕微鏡写真をとって、千分の一ミリの誤差があったら、精度は十分の一である。一キロメートルの距離を、一メートルの誤差で測れば、精度は千分の一である。この場合、一メートルの誤差のある測定の方が、千分の一ミリの誤差のある測定よりも、精密な測定なのである。

この間の事情をはっきりさせるために、有効数字という言葉がよく使われる。たいていの測定では、知りたい値を直接に測ることはめったにない。いろいろな量を測って、その組合せから、求める量を計算するのが普通である。たとえば比重を求めるために、体積と目方をそれぞれ測って、目方の数値を体積の数値で割って出すとする。この場合、割り切れることはまずないから、割算をどんどんやっていけば、桁数はいくらでも出せる。しかし目方か体積の一方または両方が、たとえば三桁しか測ってなかったら、割算で出した四桁目以下は、ほんとうかうそか分らない数字である。この場合、三桁目までは、たしかに測った量から出した意味のある数字である。このときに、有効数字は三桁であるという言葉を使う。73.1も0.00832も、ともに有効数字三桁の数である。0.52は有効数字二桁、0.520は有効数字三桁である。前の方は、三桁目は何か分らないことを示し、あとの方は三桁目まで測って、それが０であることをたしかめたという意味である。

ところでこの有効数字の桁数をたくさん出すということ、すなわちほんとうに精密な測定をすることは、なかなかむつかしいことである。その一例として、地球の形の図を第3図に示す。これはコンパスを使い、鉛筆のさきをできるだけ尖らせて描いた円である。小学生に地球の形はどうかときくと、「円い」と答える。第3図は、コンパスで描いた円であるから、「円い」ものの代表であって、小学生の答える地球の形である。

しかし地球が完全な球形でないことは、誰でも知っているとおりである。地球の表面には、ヒマラヤもあり、日本海溝もある。そういういちじるしい小凹凸のほかに、地球は南北に縮んだ楕円体になっていることは、中学校で習うとおりである。さらに大学程度になると、それもまたちがっていて、ほんとうは擬似楕円体であるということを教わる。ところが専門の地球物理学者にいわせると、地球の形は、それらのいずれでもなく「狐の色が狐色であるごとく、地球の形は、地球形である」という。

ところでこれらのいろいろな説明の中で、一番真に近い形をかけといわれると、けっきょく第3図のように、コンパスで円を描くより仕方がないのである。というわけは、次のような簡単な計算をしてみればすぐ分る。この円は直径六センチあって、線の幅は〇・二ミリである。それでこの円を地球とみると、地球の直径一万三千キロを六センチに縮尺して描いたことになる。この縮尺率で計算すると、線の幅〇・二ミリは四四キロに相当する。

ところでエヴェレストの高さは、海抜八・九キロであり、海の一番深いところといわれるエムデン海溝が、一〇・八キロの深さである。それで地球上の凹凸の差の極限は一九・七キロにすぎない。線の幅の半分以下である。従って地球表面の普通の山や海の凹凸を忠実に描いてみても、だいたいこの線の幅の十分の一程度の凹凸になってしまうので、どうにも描きようがない。それから地球は楕円体になっているといっても、球からのへだたりは案外少い量であって、赤道面内の半径よりも、南北の半径が、約二二キロ短いだけである。それで楕円体といっても、この線の幅の半分ていどの長短があるにすぎない。ちゃんとした楕円体に描けといわれたら、けっきょくコンパスで円を描くより仕方がない。擬似楕円体などというのは、もっとこまかいところの話である。それで小学生の答が一番正しいことになる。何だかごまかされたように思われる方があるかもしれないが、これは決してごまかしではない。話の秘訣は、鉛筆で描いた線には幅があることを忘れている点に、盲点があるのである。そしてこの線の幅がすなわち測定の誤差である。

ところでこの場合の誤差はどれだけかというと、六センチのところに、線の幅の半分とみて、六百分の一である。有効数字にして、三桁にすぎない。60.2ミリか60.3ミリかの区別がつかないていどである。できるだけ「完全な円」を描けといわれたら、普通にはコンパスで、円を描くより仕方がない。有効数字三桁くらいでは精度が足りないように思われるかもしれないが、それでも普通には「完全な円」でとおるのである。

それでは擬似楕円体だの、地球形だのということが、どうして分っているのかといえば、測地学が驚くべき精度に達しているからである。土地の測量は、三角法を用いて、角度を精密に測って、それで三角形を組立てて行くのである。この場合、角度はいろいろな量の中でも、一番精密に測れるもので、そのため角度の測定を基礎にしている球面天文学が、いちじるしい精度に達しているのである。ところが測地の場合には、三角測定の基線の長さがはいってくる。その長さの測定が不正確であれば、角度をいくらくわしく測っても意味がない。それで基線測量ということが、一つの重要な課題になっていて、今日では六桁の有効数字近くまで達している。基線の長さは普通四キロメートルか五キロメートルあるので、六桁目はセンチになる。それで四キロ五キロという距離を、ミリのスケールまで測って、四捨五入して、やっと六桁の有効数字が得られるのであるが、これは驚くべき精度である。

科学の全般にわたって、これだけの精度に達しているものは、すなわち六桁の精度まで得られているものは、このほかには球面天文学と、メートル原器の検定くらいのものである。メートル原器を、ある発光条件のもとでカドミウム元素から出てくる光の波長を基準として、検定したものが、現在の科学で一番精密な測定である。この測定のために、世界各国ですぐれた物理学者たちが厳密をきわめた実験をしたが、結果はなかなか一致しない。仕方なく国際間で認定をして、カドミウム基準スペクトル線の波長を6438.4696Åとしている。Å（オングストローム）は長さの単位で、一億分の一センチメートルのことである。これだと八桁の有効数字であるが、日本の渡辺博士の精密測定では6438.4682Åとなっているし、英国の測定では6438.4708Åという値が得られている。それで八桁のうち最後の二桁は確かではないので、ほんとうのところは、六桁どまりである。

六桁では足りないように思われる方があれば、それは科学を過信された結果である。五キロの距離を、ミリの単位まで測るのであるから、それ以上の精度を要求することは無理である。六桁はむしろ例外であって、普通は三桁乃至四桁の精度で、十分今日の物理学は成り立っている。もっとも物理学方面の表などをみると、結晶格子間の距離とか、いろいろな電気の量などの数字が、みな六桁ならんでいる。それで六桁の精度があたり前のような誤解を、一般の人々に与えているが、ああいう数字は、多くの場合、国際間の話し合いで決めたもので、国際法の条文と似た要素がはいっているのである。

たとえば、結晶の原子間の距離なども、六桁の数字が並んでいるが、あんなものを、そういう精度で測れるはずがないのである。原子間の距離は、Ｘ線の干渉、すなわちラウエ斑点から計算するのであるが、それにはＸ線の波長を知る必要がある。ところがＸ線の波長を、六桁まで精密に測ることは、とうていできない相談である。光の波長を測るには、光学格子を使うが、その方は十分精密な格子をつくることができるので、たいして困らない。しかしＸ線のような波長の短い波に対しては、格子は非常に細かいことが必要で、人工ではつくれない。それで結晶内の原子の配列を、格子として使いたいのであるが、それには原子間の距離が分っている必要がある。ところが原子間の距離は、Ｘ線の波長が分らないと、計算できない。いたちごっこになっているわけである。

それで岩塩の結晶について、実験で知り得る原子間距離d=2.814Åのあと、約束で０を二つつけることにして、d=2.81400Åと決めたのである。そしてこれを基準として、Ｘ線の波長を逆に決めて、その波長の値をつかって、他の結晶の原子間の距離を計算するのである。方解石の劈開面の原子間距離がd=3.02904Åであるとか、雲母はd=9.92758Åであるとかいうのは、そういう約束に基いて計算した値である。

科学上の数字に、こういう国際条約のようなものがあるということは、初耳の方もあるかもしれないが、電気の方では、もっと極端な例がある。電気の量には、抵抗、電圧、電流の三つの重要な要素があり、その間にオームの法則が存在している。それでこのうちの二つをきめれば、あとはきめられる。その二つとして、抵抗オームと、電流アンペアとをきめるのが普通であるが、これは両方とも、なかなか精密にはきめにくいものである。絶対単位は、けっきょく二つの帯電体間に働く力は、帯電量の積に正比例し、距離の二乗に逆比例するというクーロムの法則からきめることになるが、その測定は非常にむつかしく、どこでもできるというものではない。

それでシーメンス社の研究所で、次のような提案をした。純粋な水銀一四・四五二一グラムを、零度において、一〇六・三〇〇センチの長さになるように、太さ一定のガラス管に入れる。その時の抵抗を一オームとする。こういうふうに一オームという単位をきめると、あとはこの単位によって検定していけばよい。水銀はどこでも手に入るし、また一番純粋にし易いものである。ところで長さ一〇六・三〇〇センチときめたが、当時の実験の精度では、ほんとうは一〇六・三センチまでしか分っていなかったのである。しかしそれでは「精度」が足りないので、あとに０を二つつけることに、国際間の約束できめたのである。それでこの単位は、「国際（インターナショナル）オーム」と呼ばれている。その後、実験の精度が高まり、ほんとうは一〇六・三センチでは少し長すぎることが分った。一〇六・二四五センチとしなければならないことが分ったのであるが、国際単位をまたかえると、今までの表が使えなくなるので、もとのままの数値を使うことにしている。そして必要な場合は、

1国際オーム=1.000495絶対オーム

の式で換算して使うことになっている。

電流の方は、もっと人為的な要素のはいったきめ方である。硝酸銀の水溶液に、一定の電流を通して、電解を行った場合、一秒間に、〇・〇〇一一一八〇〇グラムの銀が陰極板にめっきされる場合、その電流を一アンペアとする。この場合の最後のゼロ二つも、約束できめたのである。これだけでも厄介な話なのに、この条約には、次のような附則がついている。陰極板は純粋な白金であって、銀がめっきされる量は、陰極板の一平方センチについて、〇・一グラム以下であること。陽極板の電流密度は、一平方センチについて〇・二アンペア以下であること。陰極板の電流密度は、〇・〇二アンペア以下であること。こういう人為的な約束を入れて、はじめて、一国際アンペアという単位がきまったのである。これもあとになって、少しちがっていたことが分ったが、そのままで使うことになっている。現在のところは

1国際アンペア=0.999835絶対アンペア

の換算式があてはまることになっているが、この式も前の国際オームの式も、最後の桁は少しあやしく、また今後実験が更に精密になれば、少しかわるべき性質の式である。

国際単位は、条約できめたものでも、絶対単位との関係がつけられれば、それでよいことになり、電気の方の量も、六桁あるいはそれに近い精度にまでもってこられたことになる。ただここでいいたかったことは、六桁あるいはそれに近い精度を得ることが、いかに困難な仕事であるか、という点である。それでは、それだけの精度が得られたら、われわれは自然界に対して、どれだけはっきりした知識を得たことになるのかという点が、次の問題として出てくる。

それについて、一番分り易いと思われるのは、彗星の例である。彗星には、少くも二種類あって、抛物線軌道のものと、細長い楕円軌道のものとがある。抛物線軌道の方は、一度太陽系から離れて行ったら、永久に帰ってこない。楕円軌道の方は、数十年か数百年かしたら、また見ることのできるものである。一つは永久に二度とは見られない彗星であり、今一つの方は待てばまた見られる彗星である。永久に見られないのと、待てばまた見られるのとでは、質的なちがいである。この質的にちがうものを、科学がどこまで区別し得るかは、面白い問題である。

太陽に近づいてきたときには、これらの彗星は、両方とも抛物線に近い形の軌道をとる。細長い楕円の頭の部分は、抛物線によく似た形をしていて、楕円が細長くなるほど、よく似てくる。彗星の軌道は、一部分しか測れないので、よほど精密な観測をしないと、その軌道が、楕円の一部か、抛物線の一部か区別できない。ふつうは新しい彗星が見え出すと、抛物線と仮定して、まず軌道を計算し、その後の観測をすませてから、抛物線か楕円かを調べるのである。とにかく原理的に考えれば、軌道の一部分について精密な観測をすれば、それが楕円であるか、抛物線であるかが、わかるはずである。しかし観測には必ず誤差があり、それは原理的にいって、避け得ないものである。天文の観測は、精度の点からいったら、一番進んだものであるが、それにしても、精度には限界がある。その限界から計算すると、周期が二百年以上の楕円軌道になると、抛物線との区別がつかなくなる。すなわち楕円として描いても、抛物線として描いても、「鉛筆の線の幅」の範囲内で、重なってしまうのである。観測記録には、角度にして秒の十分の一間で、記録されることになっているそうである。それから考えると、もっと長い周期のものでも、抛物線と区別できそうに思われるが、実際のところは、彗星には大きさがあって、その中心といっても、少しあいまいであり、また一つ一つの観測には誤差が伴っているので、けっきょく楕円の周期が二百年以上になると、抛物線と区別できないということは、現在天文学者の間に認められている。

こういうふうに考えてみると、二百年以上と永久とは、区別ができないというところに、科学の限界がある。今後観測がもっと精密になったら、二百年が二千年にのびるかもしれないが、原理的には同じことで、科学でいう「永久」は、数百年乃至数千年のことである。そしてわたしは、数百年がちょうどいいところで、数千年にはのびないだろうと思っている。というのは、精度が有効数字六桁というのが、ほぼ限界であって、それ以上は無理と感ぜられるからである。紙と鉛筆とで考えると、精度はいくらでも増せるように思われるが、実際に自然現象をよく見ると、なかなかそうはいかない。頭の中で考えるような、理想的な自然現象というものはないからである。

たとえば、基線測量など、うんと金をかけて、五キロメートルの距離の間を、水と氷の中に浸して、温度を厳密に一定に保ち、もっと精密な機械で測ったら、ミリメートルの十分の一くらいまで精密に測れそうに思われる。すなわち金さえかければ、できることのように思われる。しかしそれは不可能のことである。というのは、ちょっとした地震があれば、基点が一センチくらいずれるからである。十分の一ミリくらいずれる地震なら、毎日あるものと思わねばならない。そういう地震などないとしての話といってはいけないので、人体に感じないような地震なら毎日起っているのが、現実の地球である。

地球など相手にするからいけないので、実験室の中で、条件を厳密に一定にして実験をすれば、精度はいくらでも増せると、思われるかもしれない。しかしそれも駄目であって、条件をある程度以上厳密に一定にすることは、できない相談である。実験室内の測定で、一番精密に行えるのは、化学天秤による目方の測定である。これだと七桁くらいまで出せるので、長さや時間の測定とは、桁ちがいに精密な測定ができる。しかしこの測定でも、七桁目は意味がないので、六桁目でも怪しいものである。理由の一つは、測定法自身にある。化学天秤でものの目方を測るには、一方の皿に測るべきものを載せ、他方の皿に分銅を載せて、バランスするところを読む。真中についている針が垂直になって、０のところに止れば、両方の目方がひとしいことになる。しかし針はゆっくり振動していて、なかなか止らない。それで振動の両端の目盛を読みとって、停止するところを計算で出すのである。第4図(a)に示すように、左側の三回の読みの平均をとり、右側二回の読みの平均を取る。この二つの平均値のまた平均をとると、針が停止するところになる。ミリグラムの十分の一乃至百分の一のところを測るには、こうしなければならない。針が止まるまで待つよりも、この方が精密な方法なのである。ほんとうに針が止るときには、眼に見えない小さい塵が、天秤の刃のところにあっても、それが邪魔をして、停止の位置からずれたところに止るおそれが始終ある。それで停止の位置を測るには、振動させながら測らなければならない。要するに一回の測定には、ある時間がかかり、これだけの時間は、原理的にいって必要なのである。

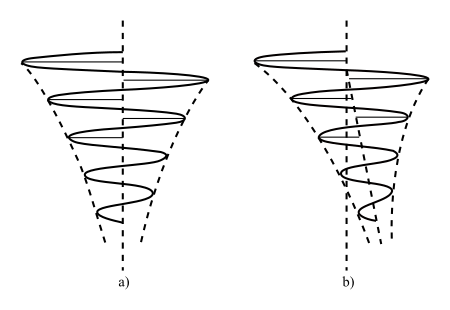
ところで天秤で木材のブロックの目方を、精密に測ってみると、針は第4図(b)のような振動をする。針の一振動の間に、もう軽くなってしまうので、五回振動するまで、待てないことになる。これでは、この程度の精密さで、目方を量ることは、不可能である。天秤のケースの中には、乾燥剤がはいっているので、木材が測定中に乾くからである。乾燥剤をとりのけ、水のはいったコップをケースの中に入れて測ってみると、針の振動は反対側にずれる。この場合は、木材は水蒸気を吸うからである。この程度の精度になると、木材などは生きたものと同じことで、一定の目方がないことになる。

それでは石や金属のようなものならば、いくらでも精密に測れるかというに、それにも限界がある。天秤が将来もっと精密になっても、測定結果として意味があるのは、せいぜい六桁くらいである。というのは、測るべき相手のものを、それ以上の精度で規定（スペシファイ）することができないからである。鉄の小片の目方を、七桁まで測っても、それはその特定の小片の、測定時における目方であって、それだけでは、物理的な意味がない。次の日測ってみると、酸化しているので、もう目方がちがう。それを拭ってやれば、拭った影響でまたちがってくる。同一の鉄の棒から、二つの標本を切り出して、比重を測ってみても、この精度になると、標本ごとにみなちがう。それでどの鉄というふうに、測るべき相手を規定することができない。

実際に存在しているもので、一番純粋であり、かつ一定の性質をもっているものは、結晶である。結晶は、特定の原子が、特定の結晶格子をつくって配列されているものである。それで純粋な結晶ならば、その物性は一定であるはずである。ところが、その物性の内で、一番はっきりしており、かつ一定であるべき結晶の比重を、精密に測ってみると、六桁のところでは、みなちがっている。それで六桁の精度までいくと、世の中に、同じものは二つとないことになる。氷の単結晶の比重は、非常によく調べられたものであるが、できるだけ完全な十一個の結晶について測った結果は、平均して、零度で〇・九一六六七である。そして各個の標本は、最後の桁で、二乃至三ちがっている。それで確かなところは、〇・九を一とみても、五桁までである。

それで六桁の精度に達すると、もはや自然界に同じものは二つとないことになる。それ以下になると、もはや再現可能の原則は成り立たない。妙ないい方になるが、自然界自身に、精度の限界があって、六桁の精度のところまでしか、科学は取り扱えないともいえよう。少くも現在の科学については、そうである。

二百年と永久の区別がつかないということは、二様に解釈できる。一つは、科学も案外無力であるという見方である。しかし同時に、二百年も先のことまで分るのであるから、非常に強力なものとも考えられる。どっちの見方をするかは、趣味の問題である。ただ科学の本質がこういうものであることを知れば、その力を正当に理解することができ、過信することはないであろう。