定性的と定量的

定性的と定量的という言葉も、科学でよく使われる。これらも科学の方法を論ずる場合には、一応考察しておくべき言葉である。

定性的というのは英語のクォーリタティヴの訳語であって、クォーリティ、すなわちものを質的に見ることである。定量的というのは、クォンティタティヴ、すなわちものの量を測って、量的に調べる場合に使われている。

科学は自然を認識する学問であると、よくいわれる。自然を認識する第一歩といえば、それは観察である。ところが普通に観察というと、すぐ小学校や中学校などで、動物とか植物とかを観察するという、あの観察を連想する。そして物理学や化学のような学問は、もはや観察などの域をとっくに離れているように考えられがちである。たとえば力学などは、ニュートンの第一法則、第二法則というものから入っていくもので、観察などという要素は、はいる余地がないように思われている。しかし観察ということは、非常に大切なことであって、このごろのように科学が進歩し、かつ専門化していても、やはり観察を無視することはできない。単なる観察などでは、新しい知識の得られる余地がないように思うのは、まちがっているのである。

通俗科学書などを見ると、この頃科学が非常に進歩して、自然界のことは、もうたいてい分ってしまったように書いてある。分子のことも分り、原子のこともわかった、原子核のことも、更に進んで素粒子のことまでも、だいたい分ったような印象を受ける。電磁波の方でも、放送などに使われる長波長のものから、短波、マイクロウェーブ、普通の光、Ｘ線、ガンマ線と、全部のものが分っている。こういう面をみると、何だか今日の物理学は、自然の究極まで究めたように思われやすい。しかし自然というものは、そう簡単なものではないのであって、普通に人間が想像する以上のものなのである。現在の科学は、なるほど今いったように、物質の究極のところまで、見きわめている面もある。しかしこれは、たとえてみると、菌糸のような発達のしかたである。非常にうねうねしながら、無数に枝分れして、ずいぶん広い範囲にわたって伸びていっている。それである方向には、非常に深く入っている。それからまた枝分れも非常にたくさんなって、ありとあらゆる分野にまで、それぞれの知識が行きわたっている。しかしその間に、取り残された領域が、まだまだたくさんある。いわば線の形をとって進歩しているのであって、面積全体をおおう、すなわち自然界全体をおおうという形にはなっていないのである。

たとえばよく例に引く話であるが、雷の電気がどうして発生するか、というようなことさえ、まだ分っていないのである。太古の人が、空を仰いで雷の電光を見て、非常に不思議に思ったのと、今日われわれが雷についてもっている知識とは、本質的にはあまりちがわないのである。空には空気と水と、そのほかに目に見えないような小さいごみくらいしかないわけであるが、そういうところで何百万ボルトの電気が起きて、あの長い火花が飛ぶということは、いかにも不思議なことである。よく雷の本体は電気の現象で、フランクリンの時代に、もう分っているというふうにいわれるが、雷の現象は電気であるといっても、それはわれわれが日常に使っている電気と同じものであることが分っただけである。もちろんそれでも鬼が太鼓を叩いているというよりも大進歩であるが、どうして大空でそのような電気が起きるのかという肝腎の不思議さは、依然として残っている。昔のシナの本などにも、雷は陰陽の気が合する時に発するものであるというようなことが書いてある。電光は陰電気と陽電気とが中和するときに飛ぶ火花であるというだけでは、昔のこの陰陽の説と、本質的にそう違っていないわけである。

雷の電気がどうして発生するかという問題は、いまだに解決がついていない。世界中の一流の学者、Ｃ・Ｔ・Ｒ・ウィルソンのような、ノーベル賞をとった人だの、英国の中央気象台長を長らく勤め、気象学の世界的な大御所とされているシンプソン博士だの、そのほかいろいろな優秀な学者たちが、ずいぶん長い年月をかけて、くわしい研究をし、お互いに論戦を続けてきたのであるが、依然として分らないのである。次ぎ次ぎと新しい説が出てきたが、それはそのときだけ一応の説明ができたように見えただけであった。新しい機械ができ、新しい観測が始められると、今までの説では、どうにも説明のできないことがでてくる。たとえば上空の電場の状態まで測ってみると、地上の観測では思いがけなかったようなことがでてくる。立派な理論と思われていたものが、次ぎ次ぎとくずれていくのである。そして最近の二、三年の間にも、また新しい理論が出ているが、それに代る理論が、またそのうちに出るであろう。

もっとはっきりした純粋な物理学の問題にも、手近かなところに、まだ分らないことがたくさんある。たとえば、氷の結晶構造すら、まだほんとうのことは分っていない。氷などは、一番身近かにあるもので、だれでも知っている。冷蔵庫の中に入っている人造の氷にしても、冬になると手洗鉢に張ったり、川に張ったりする氷にしても、すべての氷は、小さい結晶が勝手な方向に入りまじって塊になっているものである。水や氷というものは、人間生活に一番近いものであって、これなどは科学では一番よく分っているはずのものである。ところが氷の力学的性質は非常に複雑であって、その実験結果がみなちがっている。小さい結晶の集りであって、その構成要素たる単位の結晶の大きさや方向の分布が、標本ごとにみなちがうので当然のことである。

ところがもっと基本的なこと、氷塊の単位を構成している氷の結晶の構造のような問題すら、いまだに分っていないのである。これもやはりノーベル賞をもらったブラッグという大先生をはじめ、世界でも一級の学者たちが、大ぜいかかって、やっと酸素原子の配列は分ったが、水素原子がどう配列しているかは、まだ分らない。今までの知識では、氷の結晶は極性をもっていることになっているので、それならば圧電気が起きるはずなのに、いろいろ調べてみても、圧電気現象が見つからないのである。それで現在でも、氷の結晶構造のほんとうのことは、まだ分っていないといわざるを得ない。

自然界に起っている現象の中で、比較的簡単な現象を取り扱っている物理学でも、既にそうであるから、他の方面では、分らないことだらけといってよい。これは日本でも有名な内科の教授に聞いた話であるが、人間の腸の中にどういうばい菌がいて、それがどういう働きをしているか、ほとんど分っていないということである。胃腸などというものは、人間のからだの中では、一番よく分っているもののように思っていたので、この話にはひどく驚いた。食物が直接はいっていくところであるから、その働きは他の臓器よりも、ずっと分り易いように思っていたからである。腹下しなどは一番簡単なものと考えていたが、そうではないらしい。大腸菌のことは、かなりよく分っているが、あれは最後に生き残った強いやつである。消化をしたり、吸収をしたりするときに働いている、細菌とか酵素とかいう大切なものになると、いまだにその本体も作用もあまり分っていないということである。

それからよく例に出される問題であるが、植物の同化作用も、不思議な働きである。植物は炭酸ガスと水とから、澱粉を作っている。地面から水を吸い上げ、空気中から炭酸ガスをとって、いわゆる同化作用をしている。樹木が木材質をつくるのも、稲が米をつくるのも、みなこの同化作用によるのである。それには太陽光線のエネルギーが使われているが、この植物の働きによって、人間の食糧がつくられているのである。植物の葉っぱなど、ちょっと見ると、簡単なもののように思われるが、葉緑素の働きと、太陽光線とによって、水と炭酸ガスとから、どんどん澱粉を作っている。人間はこれほど科学が進歩していて、いろいろ複雑で高性能の機械をもっていても、いまだに水と炭酸ガスとから、澱粉を作ることはできない。これができるようになれば、世界の食糧問題が一ぺんに片づくわけで、そうなれば世の中がもっと住みよくなるにちがいない。ほんとうに水と炭酸ガスとから、人工で簡単に澱粉ができることになれば、それはおそらく科学の歴史の上での最大の功績の一つになるであろう。もちろんそういう重大な問題であるから、世界中のそれこそ一流の学者たちが、大勢かかって、現代科学の粋をあつめて、この問題を突っついている。従ってどんどん進歩はしているが、解決はまだ大分さきのように思われる。現代の科学の全能力をあげても、一枚の木の葉の働きには及ばないと、いえないこともない。

こういう手近かな問題、少くともわれわれの身のまわりに毎日起きている現象の中に、いまだに解けていない問題がたくさんあることは知っておく必要がある。それで自然現象自身を、注意深く観察することは、まだまだ必要である。「それは単なる観察の記録にすぎない」というような一言で、ものごとを片づけてしまってはいけないのである。一応分っているように思われることでも、自然現象というものは、もっと複雑なものだということを、始終念頭において、自分の眼で観察していくことが大切である。観察は科学の方法としては、一番原始的な方法であるが、今日の科学においても、やはり大切な一つの方法なのである。普通には観察というと、肉眼で見ることだけと思われ易い。しかし科学の場合においては、それをもう少し拡げて、顕微鏡とか、あるいは望遠鏡とか、その他の機械を用いて見るということも、もちろん含まれている。

写真というものは、科学では非常に重大な役割を果している。ある瞬間的に起った状態を、写真では固定することができる。それであとでゆっくり時間をかけて、これを調べることができるのである。十万分の一秒くらいの間に完了する速い現象でも、それを捉えることができるので、観察の武器としては、非常に有力なものである。現在の原子物理学は、原子核の物理学になっているが、このちょっと前までは、原子の構造の物理学であった。原子核の外側に電子がたくさんあって、それで原子ができているのであるが、その電子の配列、すなわち原子の構造の研究から、今日の原子物理学ができ上ったのである。電子の配列状態がちがうと、原子から出る光のスペクトラムがちがう。それでスペクトラムの研究、すなわち分光学の発達によって、原子の研究が進んだのである。

その分光学がどうして発達したかというと、少し変ったいい方をすれば、写真があったからできた学問である。ある原子なり、そのイオンなりから出てくる光を、分光器にかけて、スペクトル線に分ける。その線を、ただ目で見て、きれいな線がたくさん並んでいるというだけでは、学問にならない。一本一本の線について、その波長を精密に測って、それから原子の構造を推定するのである。それで波長を精密に測ることが大切であるが、それには写真が一番便利である。写真を使わなくても、波長の測定はできるが、それは原理的にいっての話であって、実際問題としては、それらを写真にとって、写真の上で測るから、測定が可能なのである。何千本、何万本とある線を、一本一本実験をやりながら測っていくということは、とうていできることではない。いろいろな素粒子の存在も、多くのものは、ウィルソンの霧函の中で発見されたのであるが、これも写真があっての話である。現象を固定して見せる写真、小さいものを大きくして見せる顕微鏡、遠くのものを近づけて見せる望遠鏡など、いろいろな機械を使って自然を観察する。それが科学の方法の中での基本的なものである。

もっとも観察ということは、必ずしも眼を使うことだけに限られてはいない。われわれの感覚のうちのどれかにつかまえられれば、それでよいのである。耳を使うこと、これは観察というよりも聴察といった方がよいかもしれないが、この耳を使う観察ということもあり得る。耳の方は、今まであまり研究には使われていなかったが、全くないわけでもない。たとえば、昔寺田先生が、船体の振動の研究をされたときには、耳だけで相当重要な問題が見事に解決された。船体の模型を作って、水の上に浮べておいて、太鼓のばちのような棒で、船体のいろいろなところをたたいてみた実験である。そうすると、たたく場所によって、いろいろな音が出る。その音を、各種の音叉の音と比べてみることによって、その振動数を知ることができる。それで船のいろいろなところを叩いたときの船体の振動状態を、その船体の模型について調べることができる。棒一本あれば、あとは耳を使うだけで、この問題が解決されるのである。これは有名な研究である。このように、耳を使う観察というものも、当然あってよいものなのである。そうすれば、鼻を使う観察もあってよいわけである。もちろんにおいの研究は、鼻を使うより外に方法はないので、香料の研究の方では、相当進歩している由である。

こういうふうに、観察によって、自然界に起っている現象なり、物の本態なりをよく見ておいて、その中のある性質について、いろいろな測定を行うわけである。測定ということは、ある性質が分ったときに、その性質を、どういうふうにして、数であらわすかということである。それで測定をする前に、それがどういう性質のものかということを、十分よく知る必要がある。それにはまず観察によって、ある現象なり、ものなりの性質をよく見ることが第一になさるべきことである。この第一歩のところが、すなわち定性的な研究である。測るべきある性質がきまった場合に、測定によって、それを数であらわす。数であらわされたら、それに数学を使って、知識を整理統合していく。この方の研究は、あるものの性質を、量的に調べるわけであるから、定量的の研究といわれている。

こういうふうに考えると、定性的の研究は、まず第一歩の研究であって、定量的な研究の方が、更に進んだ研究ということになる。そして事実そのとおりであるが、この初歩のところ、まず自然界を定性的に見るというようなことは、現在のように進歩した科学では、もう必要がなくなったとはいえないのである。科学のどの面においても、定量的な研究が、いつでも進歩した形であり、しかも数字の桁数がたくさん並んでいるほど精密だというふうに、一般には思われているが、そう簡単に割り切ってはいけないのである。測定された桁数が、たくさん並んでいるとき、それがほんとうに意味がある場合には、もちろんそれは精密な研究である。しかし測定しているものの性質があまりはっきりしていないような場合には、いわゆる定量的に、いくらくわしく測ってあっても、それは全く意味がない場合もある。測定によって得られた数字が、自然の実態をあらわしていないか、あるいは実態のうちごく一部の性質しかあらわしていない場合は、科学的の価値は少いのである。

その一番よい例は、プランクトンの研究などの場合に見られる。プランクトンの網を、海の中を引っぱり廻すと、その中にプランクトンがたくさん採れる。その量は、天秤で測れば、簡単に測ることができる。こういう場合には、定量的な研究は、簡単にできる。それでこの場合には、定量的の方は、初歩の研究と考えられている。このプランクトンの塊りの中には、非常にたくさんの種類のプランクトンがいる。何十種か、何百種か分らないが、とにかくたくさんの種類のプランクトンがはいっている。ところでこれらの一々のプランクトンについて、それがどういう種類のものかを確かめるとなると、非常に骨が折れる仕事になる。しかしその方が、プランクトンの本態の研究には重要であり、かつ学問的にも価値の多い研究である。それでこの場合は、定性的の研究の方が、定量的の研究よりも骨が折れ、かつ進んだ研究である。雑多な種類のプランクトンを一まとめにして、その目方が何グラムあるかを、いくら正確に測っても、学問的には、意味が少いからである。もちろん数の方も大切ではあるが、それはどういう種類のプランクトンが、どれだけいるか、というのでなければならない。定性的は初歩、定量的は進んだ研究だと思い込んでいると、ときどき錯覚に陥る場合がある。

プランクトンのような場合は、いわば例外的な話であって、普通に物理学や化学の実験の対象になっているものは、比較的簡単な性質のものが多く、そういう場合には、定性的の方は分り切っている、とそう簡単にはいえないのである。自然というものは、度々くり返して述べたように、非常に複雑なものであるから、どんな簡単そうに見えるものでも、一度は疑ってみなければならない。

ファラデーやケルヴィン卿の時代なら、ちょっとした実験をしても、大きい発見があったが、この頃のように、科学が発展してしまっては、多額の研究費を使い、大がかりな機械と設備とをもたなくては、研究らしい研究はできないと、一般には思われがちである。原子核の実験などでは、多くの場合、そのとおりであるが、科学は前にもいったように、菌糸のような恰好に発達しているので、糸と糸との間には、抜けたところが、たくさんある。現代でも、思いがけないことが、身近かなところにも、いくらもころがっている。

その一つの例として、氷の単結晶の棒に、力を加えたときに、どういう変形をするかという簡単な問題をとり上げてみよう。この研究は、アメリカでも一流の結晶学者のところで、数年前に行われていたのであるが、方法は次のとおりである。氷を四角の棒に切り出して、それを二つの楔の上にのせる。そして真中におもりをかけると、この棒はしなう。物質が軟かければ、たくさんしない、硬ければ、少ししかしなわない。それで棒のしなう量を測ると、理論的な計算によって、その物質の硬さや軟かさを示す、いわゆる弾性率を求めることができる。物体が完全な弾性体であれば、おもりを取り去ると、棒はもとどおりまっすぐになる。しかし氷などの場合には、塑性といわれる性質があって、おもりを取り除いても、少しもとに戻るだけで、氷は曲ったままの形で残る。この変形は、かけるおもりが重ければ重いほど、多いが、一定のおもりでも、おもりをかけておく時間が長いほど、変形は大きくなる。すなわち、時がたつにつれて、ずるずると形がかわっていくのである。

ところで、こういう変形は、あまりひどく変形させると、いろいろ二次的な現象の影響が出てきて、計算がむつかしくなり、棒のしなう量を測っても、それを理論的に取り扱うことがむつかしくなる。それでごく少しだけしなわせて、そのかわり、その量を精密に測って、それを理論にかけるのである。こういうやり方は、この場合と限らず、物理学の全般にわたって、いつでも採られているやり方である。

どんな変化でも、たくさんの要素の集合した結果であるが、多くの場合、その中に大きく効く要素がある。変化が小さい間は、その要素の影響が比較的強くあらわれる。そして第二、第三の要素は無視できるくらい小さい。というよりも、そういう性質の現象が、主として科学の対象になっているのである。それで、この特質を活かすために、少量の変化を精密に測る場合が多いのである。

いろいろな物質の弾性率を測るには、彎曲試験が非常によい方法で、その物質を、適当な大きさの棒型に切り出せる場合には、たいていの場合、この方法が採られる。しかし彎曲は少量にとどめておく方がよいので、しなう量は精密に測る必要がある。ちょっと考えると、それは顕微鏡を使えば、いくらでもくわしく測れそうに思われるかもしれない。事実、高倍率の顕微鏡を使えば、千分の一ミリくらいの変位は容易に測れる。しかし顕微鏡の視野の中で、棒の一点が、千分の一ミリ下って観察されても、これがそのまま、しなった量とは限らない。相当硬い物質の場合が多いので、おもりは、かなり重いものを使う。それで台も、受けの楔も、少しひずむ。棒が非常に硬ければ、少しもしなわなくても、顕微鏡の視野の中では、棒の一点は下向きに変位して見える。

それでこの場合には、次のような方法を使うのが、常識になっている。すなわち変位を直接に測らなくて、しなったために、棒の両端が、水平よりごく少し傾く。その傾く角度は、第7図のように、鏡（Ｍ）を二枚立てておくと、簡単に測れる。遠くに立ててあるスケールの読みを、鏡で二回反射させて、望遠鏡で読みとるのである。鏡が垂直に立っていた時は、Ａの目盛が、望遠鏡の視野の真中にあった。ところが、しなえば、Ｂの目盛が見える。この方法では、角度を測っているのであるから、台や楔のひずみで、棒全体が下向きに動いても、その影響はきいてこない。しかもスケールをかなり離しておくと、傾きの角度は、精密に測定でき、計算によって変位を非常にくわしく知ることができる。この方法によると、しなった量を千分の一ミリ、あるいはそれ以下まで、精密に測れるので、彎曲試験では、ほとんどの場合、この角度を測る方法が採られている。棒の真中の部分が下向きに変位する量を、直接に測るのは、原始的な方法であって、精度もいちじるしく低くなる。

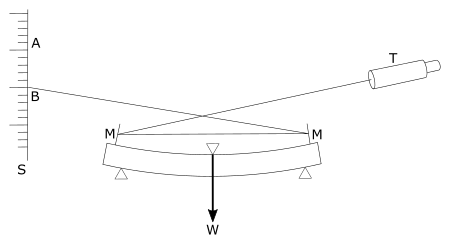
それで数年前に、アメリカで氷の単結晶（第8図）の変形の研究が始められたときにも、鏡を使う方法が採用され、いろいろくわしい測定がなされた。しかしその結果は、まちまちであって、どうも腑に落ちないことが、たくさん出てきた。とくに、結晶の主軸が垂直になるように切り出した標本では、鏡はほとんど傾かず、この方向には、氷の結晶が非常に硬いという結果が得られた。しかしそれは、今までの他の結晶について得られた知識から考えてみると、どうも腑に落ちない。

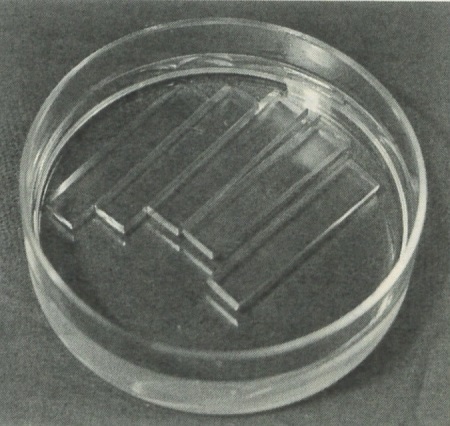
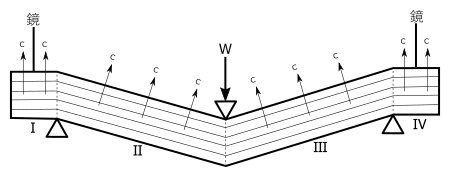
それで、原始的な方法に帰って、真中の下がる分量を直接にマイクロメーターで測ってみると、どんどん下っていくのである。けっきょく分ったことは、この場合は、棒は第10図のように、Ｖ字型に曲るのである。これならば、真中がいくら下っても、鏡は傾かないわけである。両端にはおもりがかかっていないのであるから、真中が下れば、両端がもち上りそうなものであるが、実際には、水平のままでいるのである。第11図（ｂ）の写真に、このＶ字型の変形がよく示されている。この写真は交叉偏光板の下で撮った写真であって、結晶の主軸の方向が並行に並んでいる部分は、一様な明るさあるいは暗さにうつるようにしてある。第10図で、ⅠⅡⅢⅣの四つの部分は、それぞれその部分内では、主軸ｃの方向が並行である。別の言葉でいえば、はじめ一つの単結晶であったものが、四つの単結晶に分れて、それぞれ別の行動をするのである。第11図の写真（ｃ）はもっとひどく曲げた例であって、この場合は、両端に小さいガラス板を凍りつけてあるが、それでも同じことである。

ところで、従来の「精密測定法」で、鏡の傾きの角度自身は、実測されたものであるから、問題はない。そしてその角度は、第7図の装置を用いれば、微小な角でも、きわめて精密に測定できる。そこまでは問題はないのであるが、この傾きの角度から、中央部の下った量を計算する際に、一つの仮定がはいっていたのである。それは第7図にも見られるように、棒は円形に彎曲するという仮定である。楕円でも、抛物線でも、彎曲度が小さいうちは、円と見てよいので、この仮定は正しいと考えられ、また従来いろいろな物質について測った結果も、この仮定の正当なことを認めてきた。それでこの仮定を疑う人はほとんどなく、いつのまにか、こういう仮定がはいっていることすらも忘れられてきた。

しかし自然界は、まことに複雑なもので、氷の結晶というような、身近かなものが、この仮定に従わず、Ｖ字型というような、まことに不思議な変形をするのである。

しかしここに一つ疑問が出る。第11図の(b)や(c)のような変形をするのならば、一目見ればＶ字型であることが、すぐ分るのに、それを円形と考えていたのは、変ではないか、という疑問である。事実、この程度まで曲げて見れば、一ぺんに分るのであるが、一般には、ここまでは曲げないで、測定をしていたのである。あまりひどく曲げると、いろいろな他の要素がきいてくるので、円形かＶ字型かの区別がつかない程度しか彎曲させないで、測定をして、その結果を理論的に取り扱ってきたのである。

それでは氷の場合でも、わずかの彎曲のときは円形に曲り、ひどく曲げるとＶ字型になるのではないか、という点を確かめておく必要がある。それならば、微小彎曲の場合を取り扱っているのであるから、何もＶ字型をもち込む必要はないことになる。ほんの少し曲った場合、円形かＶ字型かを、外形で区別することはむつかしい。しかしこれは交叉偏光板の下で調べれば、すぐ分ることで、第11図(a)の写真が、その例である。全体としては、まだほとんどまっすぐに見えるくらいしか曲っていないが、それでも、四つの区分が、明暗の差ではっきり出ていて、Ｖ字型であることを明らかに示している。円形ならば、境目は出ず、墨をぼかしたようにうつるはずである。

これで、氷の単結晶の場合は、特異の変形をすることが確かめられたが、こういう変形が、どうして起るかを考えてみるに、一番ありそうなことは、氷の結晶は、六方晶系に属しているが、結晶全体が一様な構造をもっているものではなく、主軸の方向に、紙を重ねたような構造をもっていて、変形は、この紙の間がずれることによって生ずる、という機巧である。そのほかに、歪みを与える力が集中したところには、特殊な結晶の境ができるということも仮定する必要がある。これは微角境界（small angle boundary）として、金属の結晶の場合では、既に知られているものである。こういう機巧を考えると、変形は、第12図に示したように起る。それだとすると、はじめに垂直に入れてかいた平行なマークＡ、Ｂは、変形後はA'、B'となり、やはり垂直でかつ互いに平行である。またはじめ滑かだった細い線は、変形後ジグザグの線になるはずである。後の研究で分ったことであるが、この紙の厚さは、約〇・〇五ミリであるから、ジグザグの階段は、〇・〇五ミリ程度のこまかいものであって、ちょっと見たところでは、直線のように見える。しかし顕微鏡写真では、この階段がよく見える。

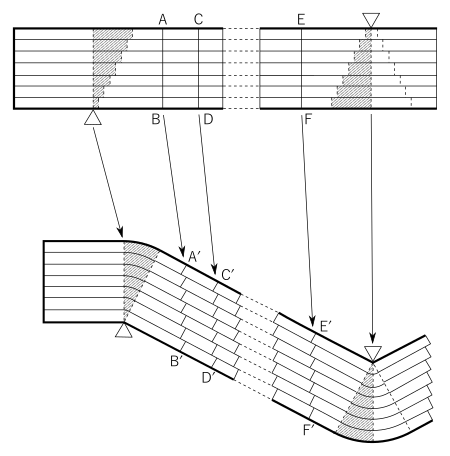
第13図は、その一例であって、水平に並んだ無数の平行線は、滑った面が写真にうつったものである。これはフーコーの影写真法という特殊撮影法を使うと、写真にうつるのである。斜めの平行線は、標本の角棒の前面につけたマークである。マイクロトームで表面を削ると、刃のこぼれによって、こういう細い条痕がつくので、それをマークとして使ったのである。写真でよく分るように、このマークは、細いジグザグになっている。この写真は、氷の単結晶の層状構造を示しているよい例である。

単結晶といえば、原子が結晶格子に従った配列をしたものと、今までは考えられていた。それに紙を重ねたような層状構造があることが分ったのは、新しい事実である。もっとも金属の結晶については、そういうことが、今までにも知られていたが、金属は内部が見えないので、こういうふうに写真にとることはできない。少くもその点では、新しい知識である。

ところでこういう発見が、どうしてできたかというと、標本の彎曲状態を、まず定性的に見た点から出発している。もし鏡の傾きを使う「精密測定」だけを、やっていたならば、くわしい数値はたくさん得られ、一見定量的な進んだ研究がなされたように見えるが、ほんとうのことは、決して分らなかったであろう。

これはごく近年の話であるが、今日のように、科学が進歩した時代になっても、定性的な研究もやはり必要であることを示す、一つの例と見ることができよう。

定性的な研究、すなわち測定の対象についてその性質を常に見守っているということは、研究の初歩の時期と限らず、全期間を通じて、常に大切なことである。